.mechanics
[Phillips, A., Introduction to Quantum Mechanics, 1997.]
.Planck’s Constant in Action
Classical physics is dominated by two fundamental concepts. The first is the concept of a particle, a discrete entity with definite position and momentum which moves in accordance with Newton’s laws of motion. The second is the concept of an electromagnetic wave, an extended physical entity with a presence at every point in space that is provided by electric and magnetic fields which change in accordance with Maxwell’s laws of electromagnetism. The classical world picture is neat and tidy: the laws of particle motion account for the material world around us and the laws of electromagnetic fields account for the light waves which illuminate this world.
This classical picture began to crumble in 1900 when Max Planck published a theory of black-body radiation; i.e. a theory of thermal radiation in equilibrium with a perfectly absorbing body. Planck provided an explanation of the observed properties of black-body radiation by assuming that atoms emit and absorb discrete quanta of radiation with energy ![]() , where
, where ![]() is the frequency of the radiation and
is the frequency of the radiation and ![]() is a fundamental constant of nature with value
is a fundamental constant of nature with value
– –
![]()
– –
This constant is now called Planck’s constant.
In this chapter we shall see that Planck’s constant has a strange role of linking wave-like and particle-like properties. In so doing it reveals that physics cannot be based on two distinct, unrelated concepts, the concept of a particle and the concept of a wave. These classical concepts, it seems, are at best approximate descriptions of reality.
..Photons
Photons are particle-like quanta of electromagnetic radiation. They travel at the speed of light ![]() with momentum
with momentum ![]() and energy
and energy ![]() given by
given by
– –
![]() and
and ![]()
– –
where ![]() is the wavelength of the electromagnetic radiation. In comparison with macroscopic standards, the momentum and energy of a photon are tiny. For example, the momentum and energy of a visible photon with wavelength
is the wavelength of the electromagnetic radiation. In comparison with macroscopic standards, the momentum and energy of a photon are tiny. For example, the momentum and energy of a visible photon with wavelength ![]() are
are
– –
![]() and
and ![]()
– –
We note that an electronvolt, ![]() , is a useful unit for the energy of a photon: visible photons have energies of the order of an eV and X-ray photons have energies of the order of 10 keV.
, is a useful unit for the energy of a photon: visible photons have energies of the order of an eV and X-ray photons have energies of the order of 10 keV.
The evidence for the existence of photons emerged during the early years of the twentieth century. In 1923 the evidence became compelling when A. H. Compton showed that the wavelength of an X-ray increases when it is scattered by an atomic electron. This effect, which is now called the Compton effect, can be understood by assuming that the scattering process is a photon-electron collision in which energy and momentum are conserved. As illustrated in Fig. 1.1, the incident photon transfers momentum to a stationary electron so that the scattered photon has a lower momentum and hence a longer wavelength. In fact, when the photon is scattered through an angle ![]() by a stationary electron of mass
by a stationary electron of mass ![]() , the increase in wavelength is given by
, the increase in wavelength is given by
– –
![]()
– –
We note that the magnitude of this increase in wavelength is set by
– –

Fig. 1.1 A photon-electron collision in which a photon is scattered by a stationary
electron through an angle ![]() . Because the electron recoils with momentum
. Because the electron recoils with momentum ![]() , the magnitude of the photon momentum decreases from pi to pf and the photon wavelength increases.
, the magnitude of the photon momentum decreases from pi to pf and the photon wavelength increases.
– –
![]()
– –
a fundamental length called the Compton wavelength of the electron.
The concept of a photon provides a natural explanation of the Compton effect and of other particle-like electromagnetic phenomena such as the photoelectric effect. However, it is not clear how the photon can account for the wave-like properties of electromagnetic radiation. We shall illustrate this difficulty by considering the two-slit interference experiment which was first used by Thomas Young in 1801 to measure the wavelength of light.
The essential elements of a two-slit interference are shown in Fig. 1.2. When electromagnetic radiation passes through the two slits it forms a pattern of interference fringes on a screen. These fringes arise because wave-like disturbances from each slit interfere constructively or destructively when they arrive at the screen. But a close examination of the interference pattern reveals that it is the result of innumerable photons which arrive at different points on the screen, as illustrated in Fig. 1.3. In fact, when the intensity of the light is very low, the interference pattern builds up slowly as photons arrive, one by one, at random
points on the screen after seemingly passing through both slits in a wave-like way. These photons are not behaving like classical particles with well-defined trajectories. Instead, when presented with two possible trajectories, one for each slit, they seem to pass along both trajectories, arrive at a random point on the screen and build up an interference pattern.
– –
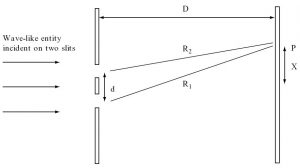
Fig. 1.2 A schematic illustration of a two-slit interference experiment consisting of two slits with separation d and an observation screen at distance D. Equally spaced bright and dark fringes are observed when wave-like disturbances from the two slits interfere constructively and destructively on the screen. Constructive interference occurs at the point ![]() , at a distance
, at a distance ![]() from the centre of the screen, when the path difference R
from the centre of the screen, when the path difference R![]() R
R![]() is an integer number of wavelengths. This path difference is equal to xd/D if
is an integer number of wavelengths. This path difference is equal to xd/D if ![]() .
.
– –
Pattern formed by 100 quantum particles

Pattern formed by 1000 quantum particles

Pattern formed by 10 000 quantum particles

Fig. 1.3 A computer generated simulation of the build-up of a two-slit interference pattern. Each dot records the detection of a quantum particle on a screen positioned behind two slits. Patterns formed by 100, 1000 and 10 000 quantum particles are
illustrated.
– –
At first sight the particle-like and wave-like properties of the photon are strange. But they are not peculiar. We shall soon see that electrons, neutrons, atoms and molecules also behave in this strange way.
..De Broglie Waves
The possibility that particles of matter like electrons could be both particle-like and wave-like was first proposed by Louis de Broglie in 1923. Specifically he proposed that a particle of matter with momentum p could act as a wave with wavelength
– –
![]()
– –
This wavelength is now called the de Broglie wavelength.
It is often useful to write the de Broglie wavelength in terms of the energy of the particle. The general relation between the relativistic energy ![]() and the momentum
and the momentum ![]() of a particle of mass
of a particle of mass ![]() is
is
– –
![]()
– –
This implies that the de Broglie wavelength of a particle with relativistic energy
![]() is given by
is given by
– –
![]()
– –
When the particle is ultra-relativistic we can neglect mass energy ![]() and obtain
and obtain
– –
![]()
.The Schrodinger Equation
.Position and Momentum
.Energy and Time
.Square Wells and Barriers
.The Harmonic Oscillator
.Observables and Operators
.Angular Momentum
.The Hydrogen Atom
.Identical Particles
.Atoms